Algorithm :: Maximum Subarray

Maximum Subarray

[Leetcode :: Maximum Subarray]
정수 배열 nums를 지정하면 합계가 가장 큰 연속적인 하위 배열(최소 1개를 포함)을 찾아 합계를 반환하십시오.

접근 방법

Brute Force

주어지는 배열은 A = [-2, 1, -3, 4, -1, 2, 1, -5, 4]로 구성돼 있다.
문제를 보면 하나의 배열안에 하위 배열들의 합을 구하는 것이라 단순하게 생각해도 반복문 2개로 풀 수 있을 것이다. A[0]부터 시작되는 하위 배열들부터 A[1]~A[N-1]로 시작하는 하위 배열들의 합 중에서 제일 큰 걸 고르면 되는데 이렇게 작성을 하면 시간 복잡도는 O(n^2^)으로 너무 느려진다.

Kadane’s Algorithm

Maximum subarray problem이라고 구글에 검색해보면 위키피디아에서 카데인 알고리즘을 설명한다. 이 카데인 알고리즘은 기존에 반복문 2개로 작성되는 시간복잡도를 낮출 수 있는 방법으로 DP의 일종이다. 전체적인 시간복잡도는 O(n)으로 배열의 원소 갯수만큼만이기 때문에 속도도 굉장히 빠르다. 단점이라고 하면 단순히 최대값을 저장하는 메모리 정도?

카데인 알고리즘은 일종의 DP이므로 이전 계산의 결과값을 저장하고 이를 활용하도록 돼 있다. 아래 그림이 카데인 알고리즘을 잘 설명하는 그림이다.

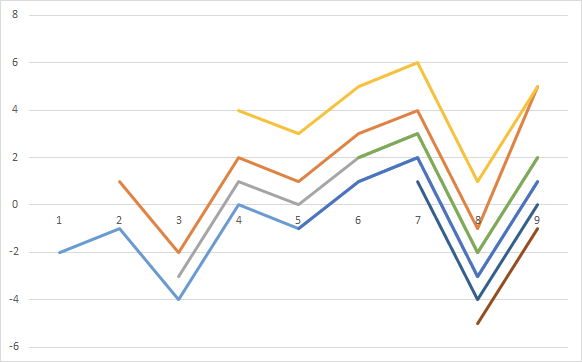
예를 들어 A[5]인 -1은 A[0]의 4번째까지의 합의 결과에 합을 한 결과다. 마찬가지로 A[2]나 A[4]도 그 전까지의 합의 결과에 합을 하고 있다. 즉, 반복문 2번 돌면서 매번 결과값을 계산하지 않고 그 전 값을 어디에(이게서는 일반 변수에) 저장하여 그 값을 참조할 수만 있다면 빠른 계산이 가능하다.

여기에 각 값을 합한것만 저장하지 않고 합한 값에 현재 값을 비교(음수 중에서도 최소의 음수를 구하기 위해)하여 최대값을 유지한 채 지금까지의 최대값과 비교하여 그 최대값을 반환하면 부분 배열의 최대 합계값을 구할 수 있다.

최종 결과

1
2
3
4
5
6
7
8
9
10
11
12

class Solution {
    fun maxSubArray(nums: IntArray): Int {        
        var bestSum = nums[0]
        var currentSum = nums[0]
        
        for (i in 1 until nums.size) {
            currentSum = maxOf(nums[i], currentSum + nums[i])
            bestSum = maxOf(bestSum, currentSum)
        }
        return bestSum
    }
}